
Explore essential Mathematics for Class 6-8 students. Build strong foundations in arithmetic, algebra, geometry, and more with our comprehensive guide
Mathematics is a crucial subject that lays the foundation for critical thinking and problem-solving skills. For students in Class 6-8, it is especially important as they transition from basic arithmetic to more complex concepts. This stage is where students start developing a deeper understanding of mathematics, which will be essential for higher education and everyday life. In this blog, we will explore the key areas of mathematics for Class 6-8, the importance of these concepts, and effective strategies for mastering them.
Key Concepts in Mathematics for Class 6-8
The mathematics curriculum for Class 6-8 covers a broad range of topics. These include:
- Number Systems:
- Whole Numbers and Integers: Understanding operations with whole numbers and integers is crucial as students begin to work with negative numbers and develop a sense of absolute value.
- Fractions and Decimals: Mastery of fractions and decimals is essential for solving problems involving parts of a whole and performing operations with non-integers.
- Algebra:
- Introduction to Variables: Students are introduced to the concept of variables, which represent numbers in algebraic expressions and equations.
- Simple Equations: Solving simple linear equations is a fundamental skill that sets the stage for more advanced algebraic problem-solving.
- Geometry:
- Basic Geometrical Concepts: Understanding points, lines, angles, and shapes forms the basis for studying geometry. Students learn to classify shapes and calculate perimeter, area, and volume.
- Coordinate Geometry: An introduction to the coordinate plane helps students graph points and shapes, leading to a better understanding of geometric relationships.
- Mensuration:
- Area and Perimeter: Calculating the area and perimeter of various shapes helps students apply mathematical concepts to real-life situations.
- Volume and Surface Area: Understanding the volume and surface area of solids like cubes, cuboids, and cylinders is crucial for spatial reasoning.
- Data Handling:
- Statistics: Students learn to collect, organize, and interpret data using measures of central tendency (mean, median, mode) and graphical representations like bar graphs and histograms.
- Probability: Basic concepts of probability are introduced, allowing students to understand the likelihood of events.
- Ratio and Proportion:
- Ratios and Proportions: These concepts are vital for solving problems involving comparisons and scaling in various contexts, such as maps, recipes, and models.
- Exponents and Powers:
- Understanding Exponents: Students learn to work with powers and exponents, which are essential for simplifying expressions and solving equations.
- Percentage:
- Calculating Percentages: Understanding percentages is crucial for problems related to discounts, interest rates, profit and loss, and statistics.
Importance of Mathematics for Class 6-8
The concepts covered in mathematics for Class 6-8 are foundational for higher-level math and many other subjects. Here’s why these concepts are important:
- Critical Thinking and Problem Solving: Mathematics teaches students to approach problems methodically, think logically, and solve complex problems step by step.
- Application in Real Life: Many of the mathematical concepts learned in Class 6-8 are directly applicable to real-life situations, such as budgeting, measuring, and analyzing data.
- Preparation for Higher Education: A strong grasp of mathematics at this stage prepares students for more advanced studies in mathematics, science, engineering, and economics.
- Building Confidence: Mastering these concepts boosts students’ confidence in their ability to tackle challenging problems, not just in math but across all subjects.
Strategies for Mastering Mathematics in Class 6-8
To excel in mathematics during these crucial years, students should adopt the following strategies:
- Practice Regularly: Consistent practice is key to mastering mathematical concepts. Students should solve a variety of problems to reinforce their understanding.
- Understand the Concepts: Instead of just memorizing formulas, students should focus on understanding the underlying concepts. This deep understanding will help them apply their knowledge to new problems.
- Use Visual Aids: Visual aids like diagrams, graphs, and models can help students better understand geometric concepts, data handling, and coordinate geometry.
- Seek Help When Needed: If students struggle with certain topics, they should not hesitate to ask for help from teachers, tutors, or peers. Addressing difficulties early prevents them from becoming bigger obstacles later on.
- Apply Math to Real Life: Encouraging students to apply mathematical concepts to everyday situations, like shopping or cooking, can make learning more engaging and relevant.
- Stay Organized: Keeping notes, formulas, and solved problems organized helps students quickly review and reinforce what they have learned.
- Practice Mental Math: Developing mental math skills can help students solve problems more quickly and improve their overall mathematical agility.
- Use Online Resources: There are many online resources available, including tutorials, practice problems, and interactive games that can make learning math fun and effective.
Introduction to Algebra and Geometry
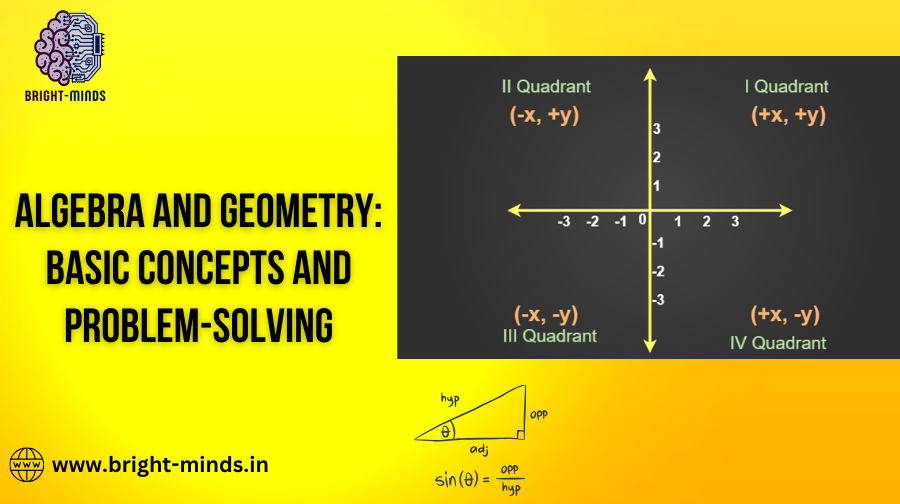
Algebra and Geometry are two of the most fundamental branches of mathematics introduced in classes 6-8. These subjects not only develop a student’s ability to think critically but also lay the groundwork for higher-level math.
1. Understanding Algebra:
- Basic Concepts:
- Algebra involves working with variables, expressions, and equations. Students learn to understand and manipulate these elements to solve problems.
- Key concepts include understanding variables, writing algebraic expressions, and solving simple linear equations.
- Problem-Solving:
- The ability to solve equations is one of the primary goals of learning algebra. Students practice solving equations with one variable and gradually move on to more complex equations involving two or more variables.
- Applications of Algebra:
- Algebra is used in various real-world scenarios such as calculating distances, budgeting, and even in sports. By relating algebraic concepts to everyday life, students can better understand the importance and utility of algebra.
2. Introduction to Geometry:
- Basic Concepts:
- Geometry deals with the study of shapes, sizes, and the properties of space. Students begin by learning about basic shapes like triangles, squares, and circles, and then move on to more complex figures.
- Concepts such as perimeter, area, and volume are essential and are often taught using visual aids and practical exercises.
- Problem-Solving:
- Problem-solving in geometry involves calculating the dimensions of various shapes, understanding congruence and similarity, and working with angles and lines.
- Students also learn to visualize geometric shapes and solve problems related to angles, lines, and polygons.
- Applications of Geometry:
- Geometry is present in everything from architecture to art. Understanding geometric principles helps students appreciate the design and structure of the world around them.
Mathematics for Class 6-8 Ratios, Proportions, and Statistics

As students progress, they are introduced to ratios, proportions, and statistics—topics that are not only important in mathematics but also have broad applications in science, economics, and everyday decision-making.
1. Ratios and Proportions:
- Basic Concepts:
- Ratios compare two quantities, while proportions show that two ratios are equal. Understanding these concepts is crucial for solving problems in mathematics and related fields.
- Students learn to solve problems involving ratios and proportions by setting up and solving equations.
- Problem-Solving:
- Students practice solving problems that involve finding the ratio between two numbers, determining proportions, and applying these concepts to real-world problems like scaling recipes or creating models.
- Applications of Ratios and Proportions:
- Ratios and proportions are used in a variety of fields, from cooking to construction, and understanding these concepts can help students in their daily lives.
2. Introduction to Statistics:
- Basic Concepts:
- Statistics involves collecting, analyzing, and interpreting data. Students learn the basics of data representation through charts, graphs, and tables.
- Key topics include mean, median, mode, and range, which are foundational concepts in statistics.
- Problem-Solving:
- Students are taught to calculate and interpret statistical measures, organize data, and create graphs and charts to represent data visually.
- Understanding how to read and interpret data is a critical skill in today’s data-driven world.
- Applications of Statistics:
- Statistics is widely used in fields such as economics, sports, medicine, and social sciences. Learning statistics helps students develop critical thinking and data analysis skills.
Real-World Applications and Advanced Math Exercises
Mathematics for Class 6-8 is not just about learning concepts in isolation; it’s about applying these concepts to solve real-world problems. This section explores how the math concepts learned can be used in practical scenarios.
1. Real-World Applications:
- Using Math in Daily Life:
- Mathematics is used in everyday activities such as shopping, cooking, and planning trips. For example, understanding ratios can help in mixing ingredients, while knowledge of geometry can help in arranging furniture.
- Students are encouraged to apply their mathematical knowledge to solve problems they encounter in their daily lives, making the subject more relevant and engaging.
- Math in Technology:
- With the advent of technology, mathematical concepts are increasingly being applied in programming, data analysis, and engineering. Understanding math can open doors to various STEM (Science, Technology, Engineering, and Mathematics) careers.
2. Advanced Math Exercises:
- Challenging Problems:
- To help students deepen their understanding, advanced math exercises are provided. These exercises challenge students to think critically and apply what they have learned in new and creative ways.
- Problems may include complex algebraic equations, geometry puzzles, and statistical data analysis, all designed to stretch students’ problem-solving abilities.
- Practice and Mastery:
- Regular practice is key to mastering math. Students are encouraged to solve a variety of problems, work on math puzzles, and participate in math competitions to hone their skills.
Conclusion
Mathematics for Class 6-8 serves as a critical stepping stone to more advanced studies. By focusing on algebra, geometry, ratios, proportions, and statistics, students build a solid foundation that prepares them for high school and beyond. With real-world applications and advanced exercises, students are not only learning math but also developing critical thinking and problem-solving skills that will benefit them in all areas of life.
you may be interested in this blog here:-
Phonics Worksheets for Kindergarten PDF Fun Literacy Stations!
