From how many hours we sleep at night to how many laps we go at the racetrack, and much more, numbers play a crucial role in our daily lives. Even and odd numbers, prime and composite numbers, fractions, decimals, rational and irrational numbers, natural numbers, integers, real numbers, rational and irrational numbers, and whole numbers are all considered numbers in mathematics. An introduction to the various kinds of numbers and its associated ideas will be provided in this chapter.
What are Numbers?
One of the fundamental elements of mathematics is a number. Counting, measuring, indexing, and maintaining order are all done with numbers. Natural numbers, whole numbers, rational and irrational numbers, integers, real numbers, complex numbers, even and odd numbers, and so on are all different kinds of numbers according to their characteristics. We can calculate the result by applying the fundamental arithmetic operations of integers. Before using numbers, tally marks were initially used. Now let’s introduce the idea of numbers and learn about their many types and characteristics..
Definition of Numbers
An arithmetic value that is expressed using a word, a symbol or a figure that represents a quantity is called a number. Numbers are used in counting and calculations.
Introduction to Numbers
The foundation of mathematics is numbers. To comprehend arithmetic, we need become friends with numbers. There are several types of numbers. Ordinal numbers, sequential numbers, odd and even numbers, whole numbers, natural numbers, integers, real numbers, rational and irrational numbers, and complex numbers are all included in our lengthy list.
We encounter the fascinating realm of factors and multiples in addition to integers. Prime numbers, composite numbers, co-prime numbers, and perfect numbers—yes, numbers may be flawless—all exist in this universe. LCM, prime factorization, and HCF.
Let’s embark on our numerical adventure. By choosing the subjects from the list below, you can proceed to investigate all of the significant issues in numbers:
| Classification | Number Names | PEMDAS |
| Number Systems | Ordinal Numbers | Consecutive Numbers |
| Integers | Natural Numbers | Whole Numbers |
| Even Numbers | Odd Numbers | Prime Numbers |
| Composite Numbers | Co-prime Numbers | Perfect Numbers |
| Fractions | Decimals | Rational Numbers |
| Irrational Numbers | Real Numbers | Complex Numbers |
| Factors | Multiples | Prime Factorization |
| Least Common Multiple (LCM) | Highest Common Factor (HCF) | Number Line |
Pre-number Math
To comprehend numbers, one must first have pre-number math abilities. The foundation for developing a strong number sense is laid by pre-number skills such as matching, sorting, categorizing, ordering, and comparing. During the preschool years, pre-number math skills are developed. Before they begin to take little steps, children learn how to stand. Similarly, the pre-number notion is crucial for kids to begin grasping mathematics. The various pre-number ideas, such as matching and sorting, comparing and ordering, classification, and shapes and patterns, will be discussed in this part.
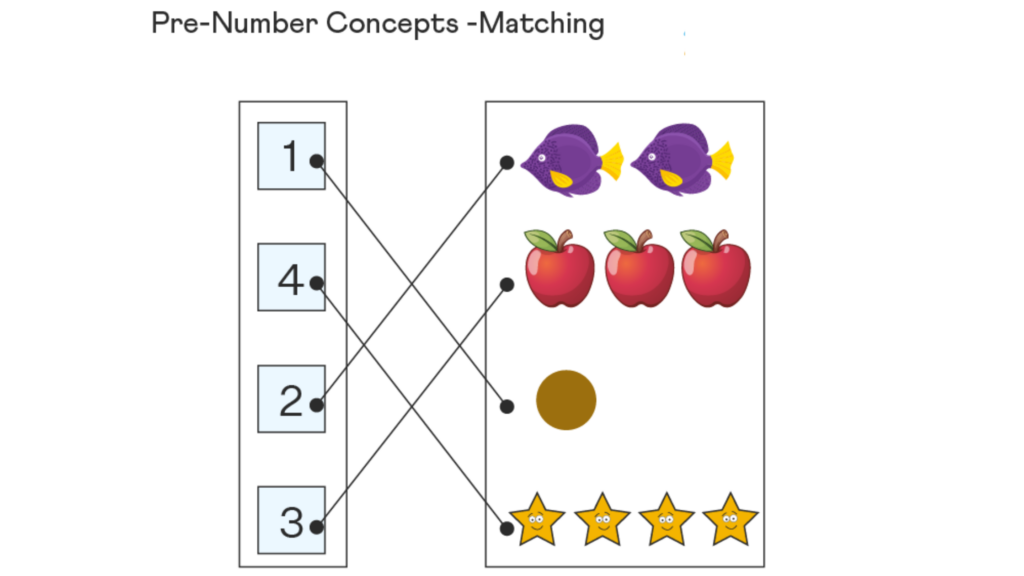
Example: Observe the figure given below which shows 2 columns. The left column displays the numbers 1 to 4. The right column displays rows of items. The numbers are matched to the quantities they represent. This is an essential skill for children aged 3 to 4 years.
Number Names
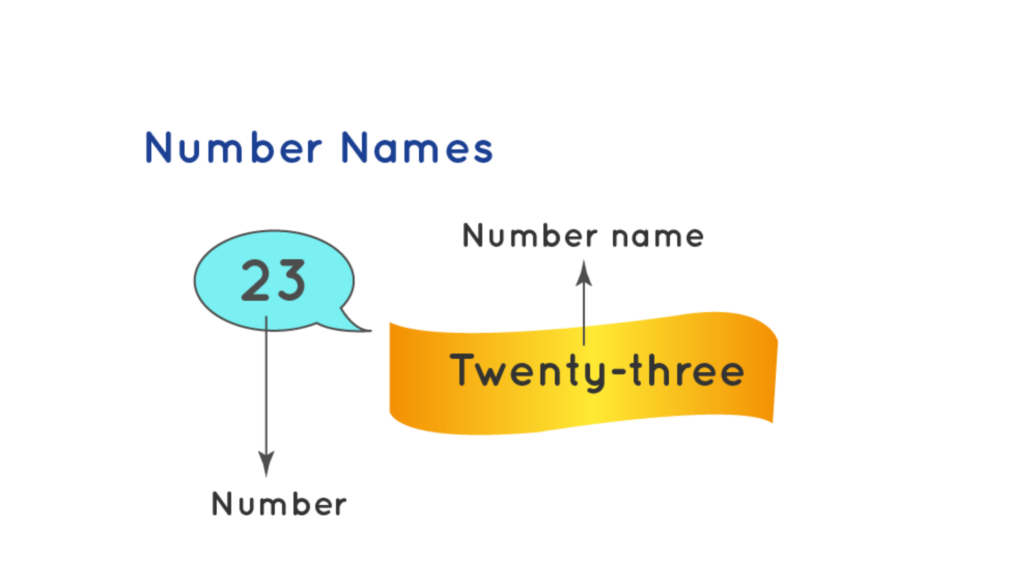
Number names are used to represent numbers in an alphabetical style. Each number is denoted by a certain word. Knowing the place value of each digit of a number is necessary in order to write it in English.
Example: Observe the figure given below which shows that 23 is written as ‘twenty-three’ in the number names form.
PEMDAS
The PEMDAS rules provide structure to nested operations and specify the order of the operations. PEMDAS, an acronym for P-Parentheses, E-Exponents, M-Multiplication, D-Division, A-Addition, and S-Subtraction, is used in mathematics.
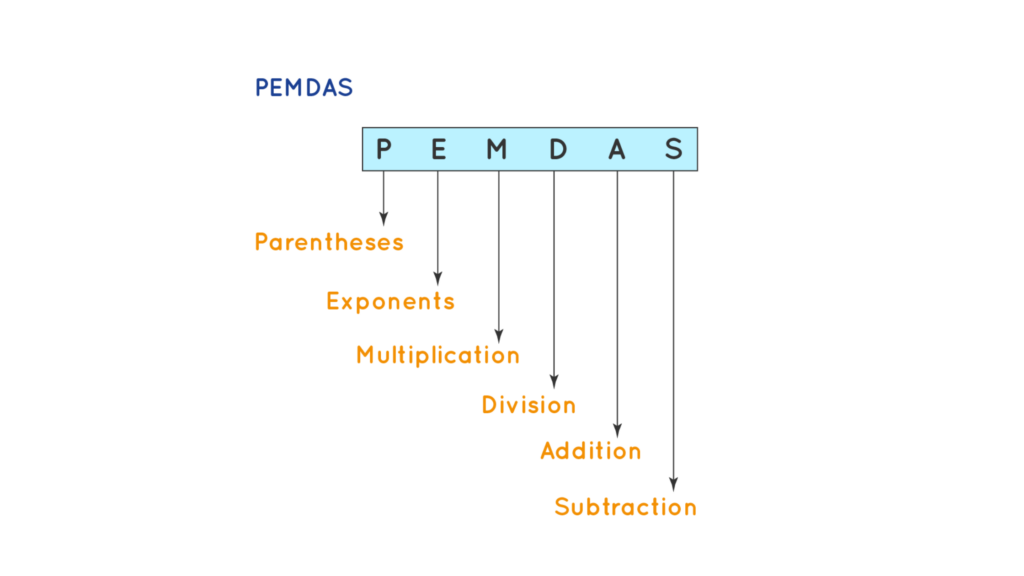
Let us learn in detail the different concepts of PEMDAS such as Addition, Subtraction, Multiplication, and Division.
Number Systems
The most widely used number system is the decimal one. Numerical values are represented by the digits 0 through 9. Every number has a place value for each digit. The conventional method for identifying integers and non-integers is the decimal number system. Numbers up to two, three, four, five, six, seven, eight, nine, and ten digits are all represented using the decimal number system.
Types of Numbers
The many kinds of numbers are determined by their characteristics. For instance, prime numbers are only divisible by 1 and the number itself, while natural numbers are counting numbers that begin at 1. Whole numbers, on the other hand, begin from 0. In the parts that follow, let’s take a closer look at the various kinds of numbers.
Numbers Chart
There are different types of numbers that are used, but the most commonly used numbers can be classified as per their unique properties. Observe the numbers chart which shows the types of numbers that are included under real numbers and all numbers apart from real numbers are termed as complex numbers.

Cardinal Numbers and Ordinal Numbers
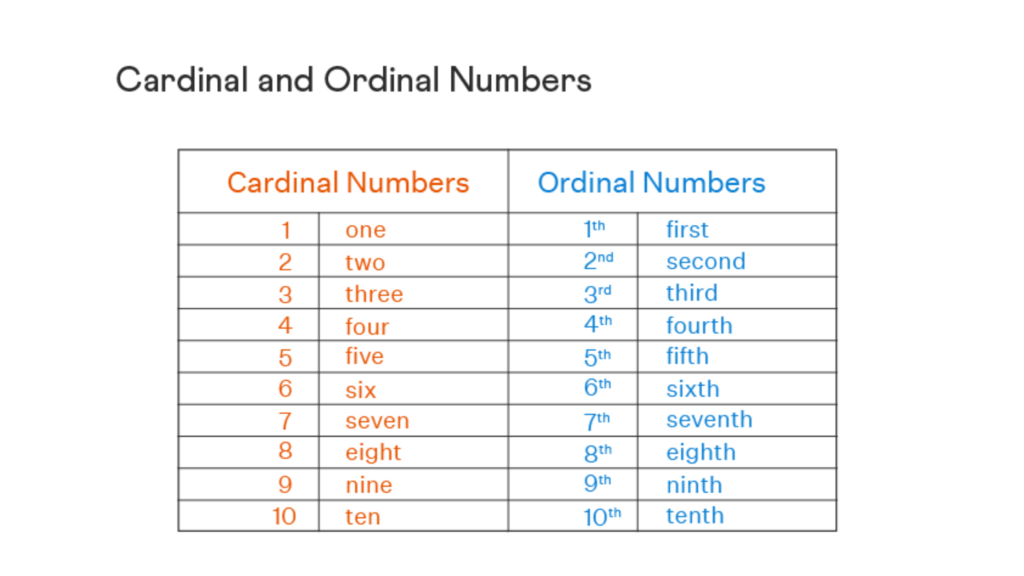
A cardinal number is a number that denotes the count of any object. Any natural number such as 1, 2, 3, etc., is referred to as a cardinal number, whereas, an ordinal number is a number that denotes the position or place of an object. For example, 1st, 2nd, 3rd, 4th, 5th, etc. It indicates the order of things or objects, such as first, second, third, fourth, and so on.
Example: Observe the table given below which shows the difference between Cardinal numbers and Ordinal numbers. Ordinal numbers help define the position of the children. Such as, Jim is the fourth child from the left.
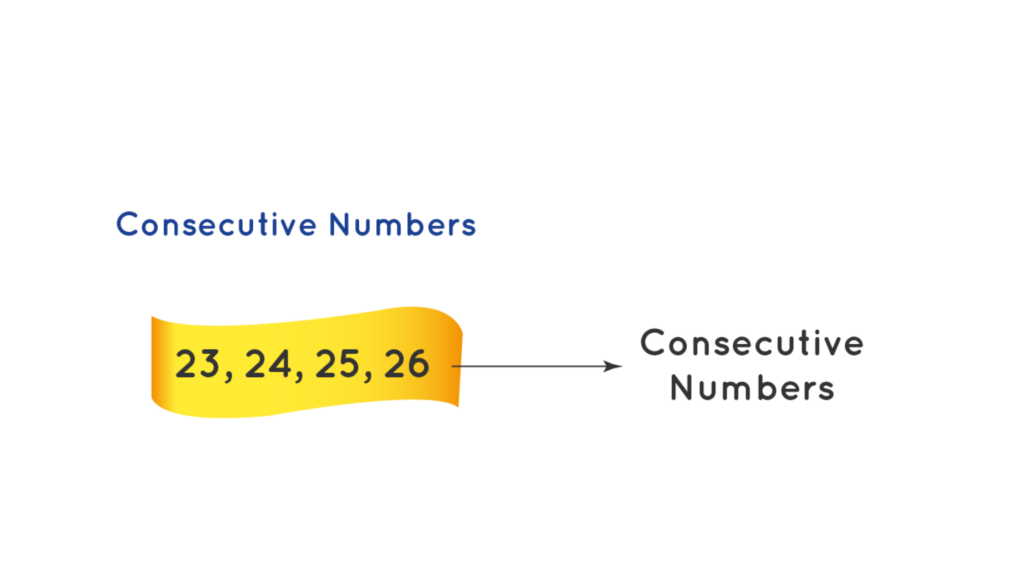
Consecutive Numbers
Consecutive numbers are numbers that follow each other in order from the smallest number to the largest number. They usually have a difference of 1 between every two numbers.
Example: Observe the figure given below which shows a list of consecutive numbers.
Integers
Numbers that are made up of both whole and negative numbers are called integers. The letter Z stands for all integers, which are devoid of fractions and decimals. Integers fill a number line. Negative integers are located on the left, and positive integers are located on the right. Remember to include the zero in between!
Z = { …., -4, -3, -2, -1, 0 , 1, 2, 3, 4,….}
Natural Numbers and Whole Numbers
A natural number is a non-negative integer and is always greater than zero. It is represented by the symbol N. It should be noted that whole numbers do not contain any decimal or fractional part. They are represented by the symbol W.

Even Numbers and Odd Numbers
Even numbers are those numbers that can be divided into two equal groups or pairs and are exactly divisible by 2. For example, 2, 4, 6, 8, 10, and so on. In other words, these are whole numbers that are exactly divisible by 2.
Example: Observe the following figure which shows that even numbers are completely divisible by 2.

Odd numbers are whole numbers that cannot be completely divided by 2. These numbers cannot be arranged in pairs. Interestingly, all the whole numbers except the multiples of 2 are odd numbers.
Example: Observe the following figure which shows that odd numbers are not completely divisible by 2 and when they are divided by 2 we get 1 as the remainder.

Prime Numbers and Composite Numbers
When a number contains exactly two factors—1 and the number itself—it is said to be prime. Prime numbers include 2, 5, 7, 11, and so forth. Any whole number larger than one that contains precisely two components—1 and itself—can be considered a prime number.
As we now know, a prime number consists of only two factors: the number itself and 1.
A composite number is one that can be divided by at least one additional integer in addition to itself and by the number 1, meaning it has more than two elements.
- Factors of 6 = 1, 2, 3, 6 (factors other than 1 and 6)
- Factors of 8 = 1, 2, 4, 8 (factors other than 1 and 8)
- Factors of 9 = 1, 3, 9 (factors other than 1 and 9)
- Factors of 12 = 1, 2, 3, 4, 6, 12 (factors other than 1 and 12)
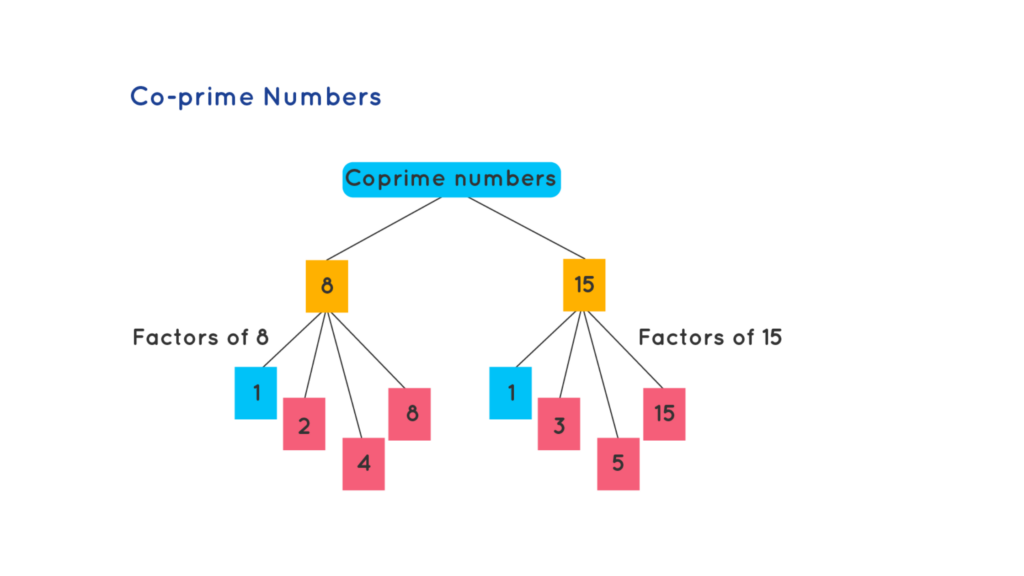
Co-prime Numbers
A pair of numbers is referred to as co-prime if they share no factors other than 1. Put differently, a group of integers or numbers that have only one common factor—that is, whose highest common factor (HCF) is 1—are co-primes. Relatively prime numbers or mutually prime numbers are other names for these. Additionally, two numbers are required to form co-primes..
Example: The following figure shows two co-prime numbers 8 and 15 that have only 1 as their common factor.
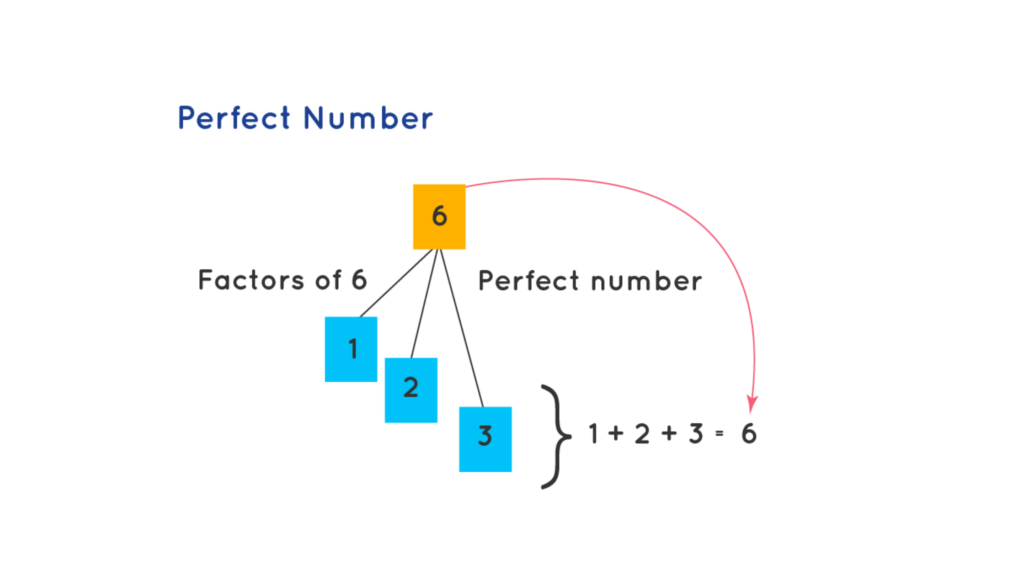
Perfect Numbers
Positive integers that equal the sum of their components, excluding the number itself, are known as perfect numbers. Stated differently, positive integers that are the sum of their proper divisors are known as perfect numbers. The sum of its appropriate divisors yields 6, the smallest perfect number: 1, 2, and 3.
Example: The following figure shows that 6 is a perfect number because the sum of its factors (1,2,3) leads to 6.
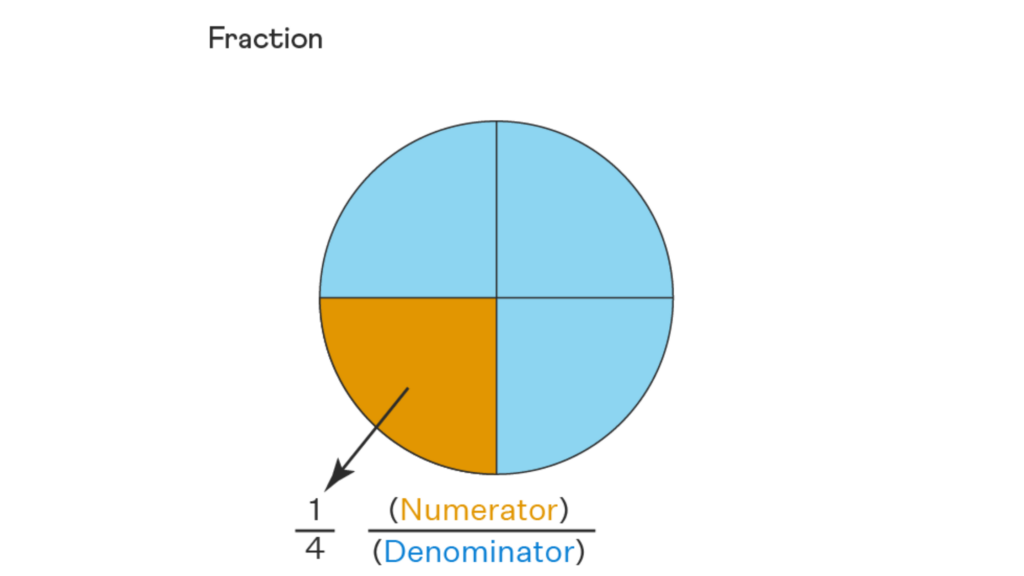
Fractions and Decimals
A fraction is a component of a whole. They are represented by integers with two parts, with a fraction bar separating each portion. The numbers at the top and bottom are referred to as the numerator and denominator, respectively.
Example: The following figure shows a fraction in which 1 is the numerator and 4 is the denominator.
Since we now understand fractions and their representation, we can examine further fraction-related subjects on pages such as Equivalent Fractions, Improper Fractions and Mixed Fractions, Fractions Addition and Subtraction, Fraction Multiplication, and Fraction Division.
How about decimals? There are two parts to a decimal number: whole numbers and fractions. A decimal point separates these sections.
Example: Observe the figure given below which shows a decimal number that has a whole number part and a fractional part.
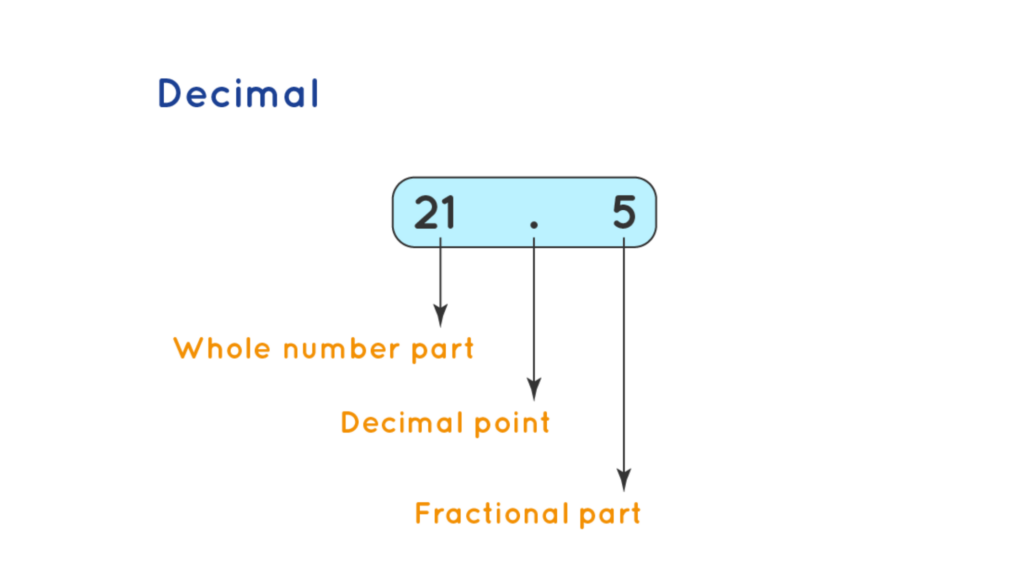
Decimals are incredibly fascinating. They can be expressed as fractions and have a whole number component. Additional decimal-related topics can be examined on pages such as Division of Decimals, Multiplication of Decimals, and Addition and Subtraction of Decimals.
you also like this
Creative Connections: Drawing and Communication Games for Children

