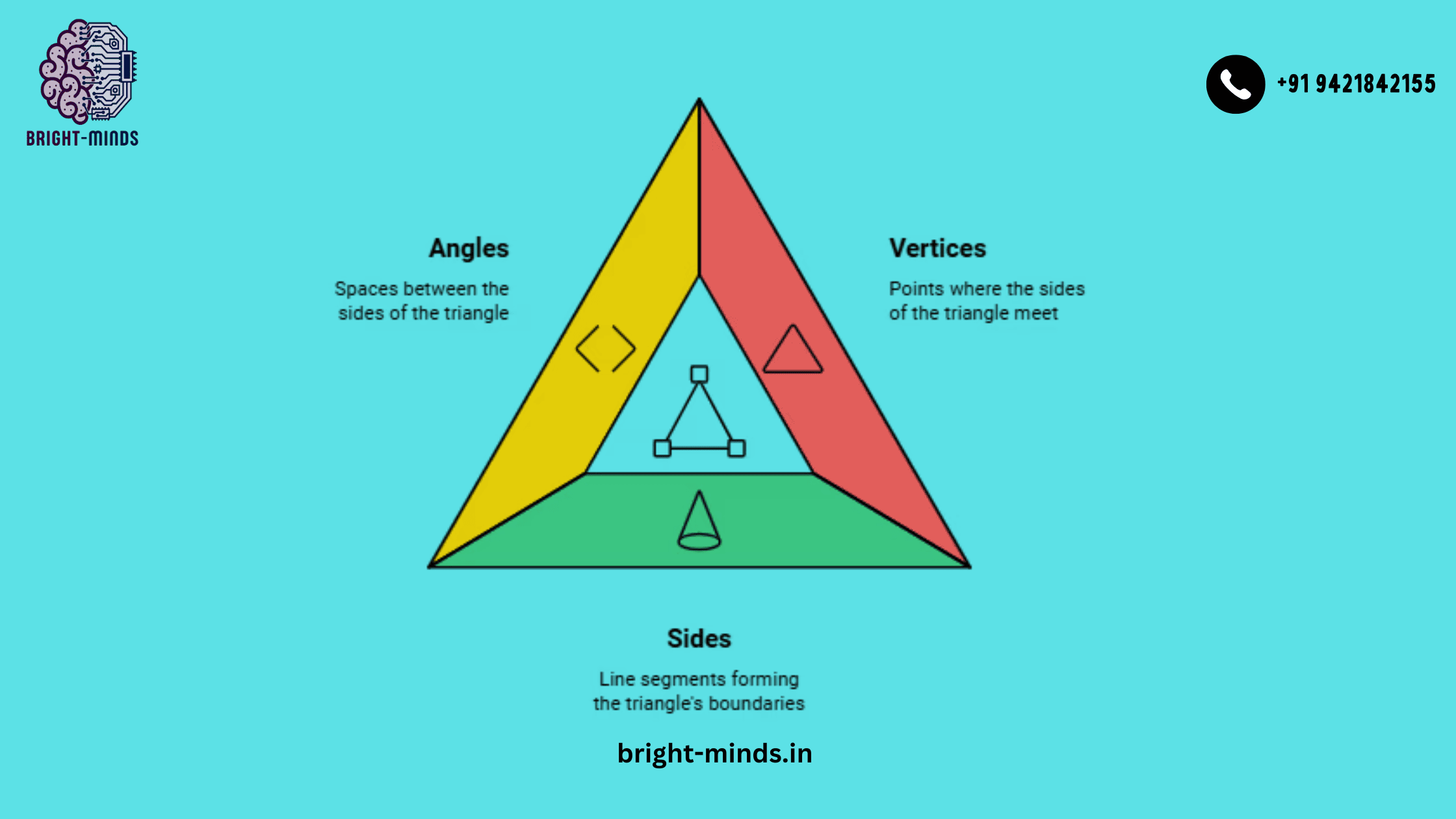
Road signs, architecture, artwork, and the natural world are all filled with triangles. However, what is so unique about triangles in mathematics? Let’s take a closer look at this straightforward but effective shape.
🔹 What Is a Triangle?
A closed figure with three sides, three angles, and three vertices is called a triangle.
For instance, the triangle is represented as △ABC if its sides are AB, BC, and CA..
🔸 Types of Triangles
Triangles can be classified based on:
✅ Sides:
- Equilateral Triangle – All sides are equal
- Isosceles Triangle – Two sides are equal
- Scalene Triangle – All sides are different
✅ Angles:
- Acute Triangle – All angles are less than 90°
- Right Triangle – One angle is exactly 90°
- Obtuse Triangle – One angle is more than 90°
📏 Important Properties of Triangles
1. Angle Sum Property
The sum of all interior angles of a triangle is always 180°.
∠A + ∠B + ∠C = 180°
2. Exterior Angle Property
An exterior angle of a triangle is equal to the sum of the two opposite interior angles.
Exterior Angle = ∠A + ∠B
3. Types of Triangles by Angles and Sides
Certain triangles can be right and scalene, or both acute and isosceles. Comprehending combinations facilitates solving geometry problems.
4. Inequality Property
The sum of any two sides of a triangle is greater than the third side.
If sides are a, b, and c, then:
- a + b > c
- b + c > a
- c + a > b
5. Pythagoras Theorem (for Right-Angled Triangle)
In a right triangle:
Hypotenuse² = Base² + Height²
✏️ Example Problem
Question: A triangle has angles 40° and 65°. Find the third angle.
Solution:
Sum of angles = 180°
Third angle = 180° – (40° + 65°) = 75°
🎲 Fun Activities to Learn Triangles
- Triangle Hunt: Assign students to locate triangle forms in the classroom or at home.
- Match the Triangle: Assign children to sort various triangle cutouts into different types.
- Give them two angles and ask them to compute the third in the Angle Sum Puzzle.
- Drawing Challenge: Assign pupils to use protractors and rulers to draw each of the three types of triangles.
🧠 Quick Revision Table
| Property | Description |
|---|---|
| Angle Sum Property | ∠A + ∠B + ∠C = 180° |
| Exterior Angle Property | Exterior = sum of opposite interior angles |
| Types by Sides | Equilateral, Isosceles, Scalene |
| Types by Angles | Acute, Right, Obtuse |
| Triangle Inequality | Sum of two sides > third side |
💡 Why Learning Triangles Matters
Geometry, trigonometry, and even architecture are built on an understanding of triangles. It also enhances reasoning and spatial thinking.
✅ Conclusion
Despite their simplicity, triangles contain important mathematical mysteries. Every student must grasp the properties of triangles in order to solve geometry problems and comprehend angles.
You may be like this:-